A side note about performance and optimization before we get started. I don’t have a ton of experience in this area, but I know that loops and branches can often be expensive. Looking at my Hull Shader for my normal render pass, I realized I had this method:

// returns true if the box is completely outside the frustum.
bool aabbOutsideFrustumTest(float3 center, float3 extents, float4 frustumPlanes[6]) {
	for (int i = 0; i < 6; ++i) {
		// if the box is completely behind any of the frustum planes, then it is outside the frustum.
		if (aabbBehindPlaneTest(center, extents, frustumPlanes[i])) {
			return true;
		}
	}

	return false;
}

That loop runs at most six times and no iteration depends on anything calculated in the previous loop. Other than making the code more readable, there really isn’t a reason to have the loop. Technically, it is dynamic and could exit early, but most of the time you’re going to do most, if not all, of the six iterations.
For that reason, I added the [unroll] attribute to the for loop. It tells the compiler to just add the code in the loop however many times (you can specify if you want) the loop will run, rather than adding branching code which tends to be more expensive to execute. There’s some good info about this and other options you can use here and here.
I was actually really shocked at the difference this little addition made. Last post, I mentioned that my frame rate was 5.1ms, or 197fps on a 2048×2048 height map with a 2048×2048 shadow map.
When I say what my frame rate is for a given set of variables, that is the slowest frame rate recorded by the Visual Studio Graphics Analyzer in the time I was running around the world.
After adding that one little attribute, I ran around the world for four minutes. The highest peak recorded in that time was 4.1ms, or 242fps. That is a savings of 1 whole millisecond, just by telling the compiler to unroll a loop! I tried this on a lark, just to see if it made any sort of difference. I think this just goes to show, experimentation is really worth it.

The Shadow Atlas

On to what I actually wanted to talk about today. I’ve gotten started on implementing Cascaded Shadow Maps. I’m not done implementing it, but I’ve made some progress and can talk a bit about where I’m at so far.
It’s been slow going, partially because I just haven’t felt very motivated to work lately; and partially because I’m trying to work out the algorithm as much as possible on my own, rather than just using someone else’s code.

So where did I start with my implementation? It makes the most sense to me to start with actually rendering the new shadow map. I’m using a method for storing the shadow cascades in a texture atlas, as suggested by Michal Valient in his ShaderX6 article ‘Stable Rendering of Cascaded Shadow Maps’. Basically, I take my original 2048×2048 shadow map, and I treat it as a 2×2 array of 1024×1024 shadow maps. This is really easy to do because you just change the size of your viewport and scissor rectangle to the new size, and then have 4 possible viewports with offsets that line up in the shadow atlas. By running a render pass for each viewport, you wind up filling the atlas.
Let’s take a look at what that looks like. Our initial viewport was defined like so:

mShadowMapViewport.TopLeftX = 0;
mShadowMapViewport.TopLeftY = 0;
mShadowMapViewport.Width = 2048;
mShadowMapViewport.Height = 2048;
mShadowMapViewport.MinDepth = 0;
mShadowMapViewport.MaxDepth = 1;

mShadowMapScissorRect.left = 0;
mShadowMapScissorRect.top = 0;
mShadowMapScissorRect.right = 2048;
mShadowMapScissorRect.bottom = 2048;

cmdList->RSSetViewports(1, &mShadowMapViewport);
cmdList->RSSetScissorRects(1, &mShadowMapScissorRect);

The first step is to halve the width and height values so that our shadow map only takes up one quarter of the shadow map. Let’s look at the result:

So rendering at one quarter size was easy. How about rendering multiple times to each viewport? I’m combining these code chunks like they’re in the same function, but I actually predefine the viewports on init and then the render code is in my DrawShadowMap() method.

int w = width / 2;
int h = height / 2;
for (int i = 0; i < 2; ++i) {
	for (int j = 0; j < 2; ++j) {
		// create a viewport and scissor rectangle as the shadow map is likely of different dimensions than our normal view.
		maShadowMapViewports[i * 2 + j].TopLeftX = i * w;
		maShadowMapViewports[i * 2 + j].TopLeftY = j * h;
		maShadowMapViewports[i * 2 + j].Width = (float)w;
		maShadowMapViewports[i * 2 + j].Height = (float)h;
		maShadowMapViewports[i * 2 + j].MinDepth = 0;
		maShadowMapViewports[i * 2 + j].MaxDepth = 1;

		maShadowMapScissorRects[i * 2 + j].left = i * w;
		maShadowMapScissorRects[i * 2 + j].top = j * h;
		maShadowMapScissorRects[i * 2 + j].right = maShadowMapScissorRects[i * 2 + j].left + w;
		maShadowMapScissorRects[i * 2 + j].bottom = maShadowMapScissorRects[i * 2 + j].top + h;
	}
}

for (int i = 0; i < 1; ++i) { cmdList->RSSetViewports(1, &maShadowMapViewports[i]);
	cmdList->RSSetScissorRects(1, &maShadowMapScissorRects[i]);

	// mDrawMode = 0/false for 2D rendering and 1/true for 3D rendering
	T.Draw(cmdList, true);
}

An Aside about Geometry Shaders

I tried actually rendering all four quarters in one render pass by using a Geometry Shader as well. You can set multiple viewports and scissor rectangles using the RS methods.

cmdList->RSSetViewports(4, maShadowMapViewports);
cmdList->RSSetScissorRects(4, maShadowMapScissorRects);

Your Geometry Shader is compiled exactly like any other shader. If you use Visual Studio, you can just use the template to create a basic shader. In the GS_OUTPUT structure, you need to define a uint scalar variable with the SV_ViewportArrayIndex semantic set.

struct GSOutput
{
	float4 pos : SV_POSITION;
	uint viewport : SV_ViewportArrayIndex;
};

You can then set that viewport value to whichever viewport you want the triangle you’re outputting to show up on.

[maxvertexcount(3)]
void main(triangle float4 input[3] : SV_POSITION, inout TriangleStream<GSOutput> output) {
	for (uint i = 0; i < 3; i++) {
		GSOutput element;
		element.pos = input[i];
		element.viewport = 1;
		output.Append(element);
	}
}

If you want/need to output to multiple viewports, you need to specify that more than three vertices (one triangle) can come out of this shader. Then you need to understand that the Geometry Shader is actually outputting a triangle strip, so if you want to output a separate triangle or to a separate viewport, you need to cut the strip.

[maxvertexcount(6)]
void main(triangle float4 input[3] : SV_POSITION, inout TriangleStream<GSOutput> output) {
	for (uint i = 0; i < 3; i++) {
		GSOutput element;
		element.pos = input[i];
		element.viewport = 1;
		output.Append(element);
	}

	output.RestartStrip();

	for (uint i = 0; i < 3; i++) {
		GSOutput element;
		element.pos = input[i];
		element.viewport = 3;
		output.Append(element);
	}
}

I don’t have screen shots of this, but it would just render the same scene to two different quadrants of the shadow map, based on how I had defined the viewports previously.
I thought this would be faster than running four passes to build the shadow map. After all, this only requires one pass through the tessellation stages to build all of the geometry. But for some reason even just rendering to one viewport took as long as rendering to all four. And rendering to two viewports took at least twice as long. Something about what the Geometry Shader stage adds to the pipeline really killed it.
I will say that I didn’t attempt to unroll those loops in the shader. Maybe I would have gotten crazy gains again. Once I’ve completed implementing CSM I’ll revisit this and maybe having a better understanding of the algorithm will lead to me figuring this out.

Figuring Out View Frusta

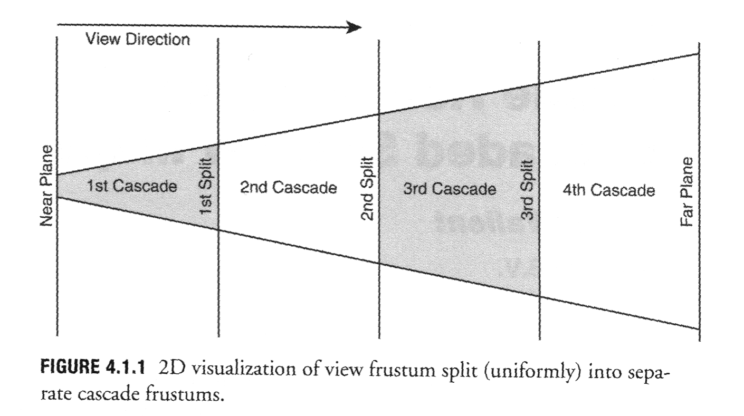
So at this stage I can render to each of the four cascades of our shadow map, but we’re still just rendering the exact same thing to each. Also, we’re still rendering using this light frustum which is completely detached from the view frustum. The point of CSM is that the cascades are loosely fit to the view frustum so that we better optimize the use of the shadow map resolution we have, and also hopefully can cull objects in the scene that won’t actually contribute to the visible shadows.
Our next step, therefore, is to define the view/projection matrices for each of our cascades, based on the view frustum. The idea behind the algorithm is that the view frustum is broken up into a series of frusta with different near and far planes.

For each of the frusta we need to find the bounding sphere, similar to how we use a bounding sphere of the scene. This can be used to create a rotation invariant light frustum, only now it will be sized more closely to the current frustum.
I started off by just trying to get the math working for the entire view frustum. Once I have that working, I can then split it up into the individual cascades.
I don’t really have a very clean interface for working with frusta yet. My view frustum is currently just an array of 6 XMFLOAT4 vectors that represent the planes of the frustum. That was calculated from the view/projection matrix in Part 10. My problem is that now I actually need the corners of the frustum, and I need a way to get them. The way I’m currently using seems to work fairly well, and is simple in concept.
[EDIT]
It turns out the method for calculating a view frustum that I came up with here is completely wrong. I’m still working on getting the CSM working properly, but I will talk about what’s wrong with this method and what I’m using now in my next post. The bounding sphere stuff is fine. It’s the first bit where I create the frustum points themselves.
[/EDIT]
We start with the frustum in light space, where it is a unit cube with dimensions [-1, 1] and the scene is warped to fit it. It is trivial to define the eight corners of the frustum for this case.
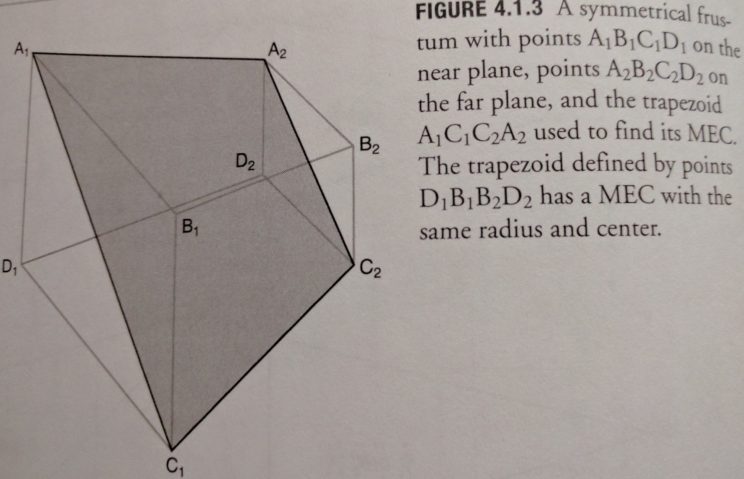
We can then transform our vertices by the inverse of the view/projection matrix to project them into world space. At that point, the points should represent a sort of truncated pyramid. In our case, as in the case represented in Michal Valient’s ShaderX6 article mentioned earlier, the pyramid is symmetric. This means that if we find the minimum enclosing circle of the points of the trapezoid defined by cutting the pyramid in half diagonally, we’ll have our bounding sphere.

It took me a while to figure out how to get a bounding sphere from that. I kept trying to find a nice clean solution using all four points, but the minimum enclosing circle algorithms I was finding either meant using a third party library or writing a bunch of code I didn’t feel like writing.
And then something mentioned in a post on GameDev.net that I had skimmed over earlier finally clicked. A dude (I’m assuming) called Postie had left a simple post with no details.

You could try calculating the circumcircle from any 3 of the points. Because the shape is symmetrical the left out point should also be on the circle, satisfying your requirement for a minimum bounding sphere.

That was enough, though. All I need to do is take three vertices from that frustum and I can find the circumcenter of the triangle. The circumcenter is the point equidistant from all three vertices of the triangle. It is also defined as the center of a circle passing through the three vertices of the triangle. It can be found by finding the intersections of the perpendicular bisectors of the edges of the triangle. And as Postie says, that circle (or sphere) will contain all of the other points of the frustum as well, because our frustum is symmetric. I don’t have a good way of drawing this, so check this page out instead.
Using the labelling in the diagram above, I chose C₁, C₂, and A₁ as they represent the furthest points apart in the frustum. Right now, projecting the points into world space and then finding the bounding sphere is all done in one big ugly function. I’ll clean things up later.

void Camera::GetBoundingSphereByNearFar(float near, float far, XMFLOAT4& center, float& radius) {
	// get the current view matrix
	XMMATRIX view = XMLoadFloat4x4(&mmView);
	// calculate the projection matrix based on the supplied near/far planes.
	XMMATRIX proj = XMMatrixPerspectiveFovLH(XMConvertToRadians(60.0f), (float)mWidth / (float)mHeight, near, far);
	XMMATRIX viewproj = view * proj;
	XMMATRIX invViewProj = XMMatrixInverse(nullptr, viewproj); // the inverse view/projection matrix
	
	// 3 points on the unit cube representing the view frustum in view space.
	XMVECTOR nlb = XMLoadFloat4(&XMFLOAT4(-1.0f, -1.0f, -1.0f, 1.0f));
	XMVECTOR flb = XMLoadFloat4(&XMFLOAT4(-1.0f,  1.0f,  1.0f, 1.0f));
	XMVECTOR frt = XMLoadFloat4(&XMFLOAT4( 1.0f,  1.0f,  1.0f, 1.0f));

	// transform the frustum into world space.
	nlb = XMVector3Transform(nlb, invViewProj);
	flb = XMVector3Transform(flb, invViewProj);
	frt = XMVector3Transform(frt, invViewProj);
	
	XMFLOAT4 _nlb, _nrt, _flb, _frt;
	XMStoreFloat4(&_nlb, nlb);
	XMStoreFloat4(&_flb, flb);
	XMStoreFloat4(&_frt, frt);

	// find circumcenter of triangle formed by these three points on the frustum.
	XMVECTOR a = nlb / _nlb.w;
	XMVECTOR b = flb / _flb.w;
	XMVECTOR c = frt / _frt.w;
	XMVECTOR ac = c - a;
	XMVECTOR ab = b - a;
	XMVECTOR N = XMVector3Normalize(XMVector3Cross(ab, ac));
	XMVECTOR halfAB = a + ab * 0.5f;
	XMVECTOR halfAC = a + ac * 0.5f;
	XMVECTOR perpAB = XMVector3Normalize(XMVector3Cross(ab, N));
	XMVECTOR perpAC = XMVector3Normalize(XMVector3Cross(ac, N));
	// line,line intersection test. Line 1 origin: halfAB, direction: perpAB; Line 2 origin: halfAC, direction: perpAC
	N = XMVector3Cross(perpAB, perpAC);
	XMVECTOR SR = halfAB - halfAC;
	XMFLOAT4 _N, _SR, _E;
	XMStoreFloat4(&_N, N);
	XMStoreFloat4(&_SR, SR);
	XMStoreFloat4(&_E, perpAC);
	float absX = fabs(_N.x);
	float absY = fabs(_N.y);
	float absZ = fabs(_N.z);
	float t;
	if (absZ > absX && absZ > absY) {
		t = (_SR.x * _E.y - _SR.y * _E.x) / _N.z;
	} else if (absX > absY) {
		t = (_SR.y * _E.z - _SR.z * _E.y) / _N.x;
	} else {
		t = (_SR.z * _E.x - _SR.x * _E.z) / _N.y;
	}

	XMVECTOR Circumcenter = halfAB - t * perpAB;
	XMVECTOR r = XMVector3Length(frt - Circumcenter);

	XMStoreFloat(&radius, r);
	XMStoreFloat4(&center, Circumcenter);
}

That seems to be producing what I want. In my original method for calculating the matrices for transforming into the light’s view/projection and texture spaces, I was using the bounding sphere for the scene. Now I use the bounding sphere calculated from this. To test, I switched back to just a single shadow map.

There’s a lot of wasted space. I don’t know that it’ll be a big deal once I’ve actually added the four smaller cascades. This is for a very large view frustum (near = 0.1, far = 3000), so smaller may be better. That being said, Jonathan Blow talks about this method and the amount of wasted space being due to the fairly large field of view values we tend to use. I’m only using 60°, which is pretty small compared to what he talks about using, but the problem remains. He goes on to show how his team improved on the memory usage for this. I don’t plan on implementing anything like that. Memory usage isn’t a priority in this project.

So that’s as far as I’ve made it so far. Next post, I should have the cascades and their matrices defined. Hopefully I will also have figured out how to choose a cascade in the shaders to get your shadow info from. Wolfgang Engel talks about a neat sounding method that was supposed to be in ShaderX7, but I can’t find it in that book. There is, however, a method in that book I may try. But I’ll also try the method he outlined as well.

For the latest code, check GitHub.

Traagen

• Cascaded Shadow Maps,
• CSM,
• direct3d,
• direct3d 12,
• directx,
• directx 12,
• height map,
• render,
• shadow map,
• shadow mapping,
• terrain